A menudo nos vemos obligados a resolver problemas con restricciones en la vida real, como por ejemplo: comprar en varias tiendas lejanas, planificar y organizar los gastos de las vacaciones o empaquetar las cosas en cajas durante una mudanza. Resolver estos problemas con restricciones no siempre es fácil. Más concretamente, cuando se trata de optimizar un conjunto de criterios como el tiempo, el coste o el espacio. Para muchos problemas, el conjunto de soluciones posibles es muy grande, lo que hace imposible comparar las posibles soluciones en un tiempo razonable. La automatización de la resolución es, por tanto, necesaria, aunque también represente un verdadero reto para las máquinas.
¿Qué son los problemas de satisfacción de restricciones?
Este tipo de problema es ampliamente investigado en la literatura bajo el nombre de " Problema de satisfacción de restricciones (CSP)" [1,3-6], que se define formalmente por una tripleta (X, D, C) donde :
- X = {X_1,X_2,...,X_N} es un conjunto de variables del problema.
- D es una función de dominio que asocia a cada Xi su dominio D(X_i) (posibles valores de X_i).
- C = {C_1,C_2,...,C_M} es un conjunto de restricciones del problema.
Una restricción está definida por un par (V,R) donde:
- V = {V_1,V_2,...,V_R} es el conjunto de variables relacionadas con la restricción.
- R es una relación que define el conjunto de tuplas que satisfacen la restricción.
Para definir un problema como CSP, debemos responder a tres preguntas clave:
- ¿Cuál es el conjunto de variables de nuestro problema?
- ¿Cuál es el dominio de cada variable de nuestro problema?
- ¿Y cómo se define una restricción?
Ya hemos respondido a estas tres preguntas para un problema de optimización de la planificación de los servicios de atención domiciliaria [2] y un problema de optimización de la planificación de los recursos materiales y humanos para las intervenciones de mantenimiento. En este artículo detallamos el lenguaje que propusimos para definir las restricciones.
Un lenguaje de restricciones para CPS
Propusimos un lenguaje flexible y expresivo para representar las restricciones en forma de predicados que pueden incluir variables, constantes y funciones del problema.
Una restricción se refiere a una variable V, está definida por un conjunto de reglas de restricción aplicadas a la variable V. La combinación de estas reglas de restricción produce un lenguaje muy expresivo para construir restricciones. Este lenguaje debe ser cuidadosamente definido, cuanto más expresivo sea el lenguaje, más permite representar más restricciones, pero la evaluación de estas restricciones será más difícil y larga. Cuanto menos expresivo sea el lenguaje, menor será la posibilidad de expresar restricciones, pero la evaluación de estas restricciones será fácil y rápida.
Definición de una restricción
Una restricción está definida por una pareja:
- V es la variable afectada por la restricción, cada restricción afecta a una variable.
- R=(R_1,R_2,...,R_N) es el conjunto de reglas de restricción aplicadas a la variable V.
Se define una regla de restricción R para restringir el dominio de una variable V. Esta restricción se lleva a cabo mediante cuatro operadores posibles: "mayor que" para seleccionar valores mayores que el operando, "menor que" para seleccionar valores menores que el operando, "igual a" para redefinir el dominio de la variable con un conjunto de operandos y "diferente de" para seleccionar valores diferentes al conjunto de operandos. Los operandos de un operador pueden ser constantes, variables del CSP o la combinación de ambas.
Una regla de restricción sólo se aplica si todas las condiciones asociadas a la regla son "verdaderas".
Una regla de restricción R está definida por un cuarteto (T,RC,RV,D):
- T es el tipo de la regla de restricción.
- RC=( RC1, RC2,..., RCM) es el conjunto de constantes de la regla de restricción.
- RD=(RD1, RD2,..., RDP) es el conjunto de variables de la regla de restricción.
- D=(D1,D2,..., DZ) es el conjunto de condiciones de la regla de restricción.
Las condiciones de una regla de restricción se utilizan cuando la aplicación de la regla de restricción depende del valor de otra variable del problema. Las condiciones se evalúan al asignar la variable para redefinir su dominio.
Una condición se define mediante un triplete :
- T es el tipo de condición.
- OC=(OC1, OC2,..., OCM) es el conjunto de constantes de la condición.
- OV=(OV1, OV2,..., OVM) es el conjunto de variables de la condición.
Aplicación de una restricción
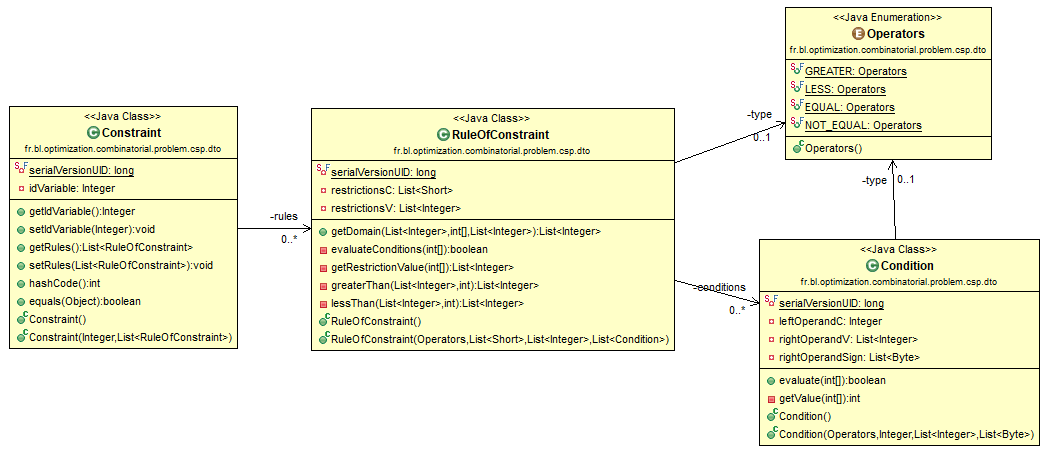
Las restricciones se implementan como clases Java (La Figura 1):
- Clase de restricción: es la clase principal. Contiene la variable afectada por la restricción y el conjunto de reglas de restricción asociadas a la variable.
- Clase RuleOfConstraint: permite definir las reglas que permiten restringir el dominio de la variable. Está definida por su operador, sus operandos y un conjunto de condiciones a comprobar antes de la evaluación de la regla. También contiene la función "getDomain (...)" que evalúa la regla para devolver el nuevo dominio de la variable.
- Clase de condición: define la condición que debe satisfacerse antes de la evaluación de una regla de restricción. Se define mediante un operador de condición y un conjunto de operandos (constante y variables).
Todas las limitaciones del contexto de la planificación de los servicios de atención domiciliaria o de las intervenciones de mantenimiento pueden expresarse con nuestra aplicación.

Conclusión y perspectiva
En resumen, hemos propuesto un lenguaje de restricciones para definir las restricciones de un CSP. Este lenguaje abarca una familia de sublenguajes de la lógica de primer orden. Nos permite tratar todas las restricciones encontradas en el contexto de la planificación de los servicios de atención domiciliaria o de las intervenciones de mantenimiento.
El siguiente objetivo de nuestro trabajo es demostrar que nuestro lenguaje de restricciones permite expresar todas las restricciones de un CSP. Tenemos previsto definir métricas sobre las restricciones para mejorar la estrategia de selección de variables y trabajar en el mecanismo de evaluación de las restricciones para mejorarlo. También estudiaremos lo que se hace en los CSP en términos de filtrado de dominios de variables, representación y gestión de restricciones.
Referencias
[1] Sally C Brailsford, Chris N Potts y Barbara M Smith. 1999. Constraint satisfaction problems: Algorithms and applications. Eur. J. Oper. Res. 119, 3 (1999), 557-581.
[2] Yahia Chabane, Christophe Bortolaso y Mustapha Derras. 2019. Cuando las hormigas cuidan de los humanos: ACO para la optimización de la planificación de los servicios de atención domiciliaria. En Estudios en tecnología e informática de la salud.
[3] Christodoulos A Floudas y Panos M Pardalos. 1990. A Collection of Test Problems for Constrained Global Optimization Problems. Springer.
[4] Kim. Marriott y P J Stuckey. 1998. Programming with constraints : an introduction. MIT Press Cambridge, Mass.
[5] Francesca Rossi, Peter van Beek y Toby Walsh (Eds.). 2006. Handbook of Constraint Programming. Elsevier.
[6] Christine Solnon. 2010. Ant Colony Optimization and Constraint Programming. Wiley.