Propriétés incrémentielles
Kevin Ducharlet est candidat au doctorat dans l'équipe DRIT. Depuis un an et demi, il a commencé sa thèse intitulée : "Certification et confiance dans les données des capteurs : détection des valeurs aberrantes et anormales dans les séries chronologiques." Les données des capteurs sont générées par des dispositifs qui mesurent le comportement d'un bien physique. Ces informations peuvent être utilisées pour informer ou introduire un autre système ou pour guider un processus. L'objectif final de son projet est de certifier la qualité des données des capteurs en développant un logiciel de détection d'anomalies proposant une solution au logiciel avec lequel il est couplé..
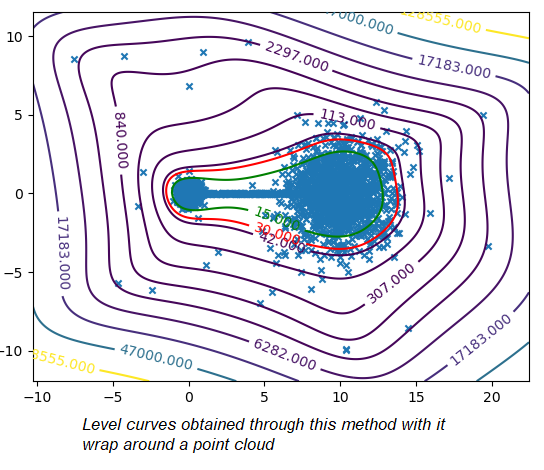
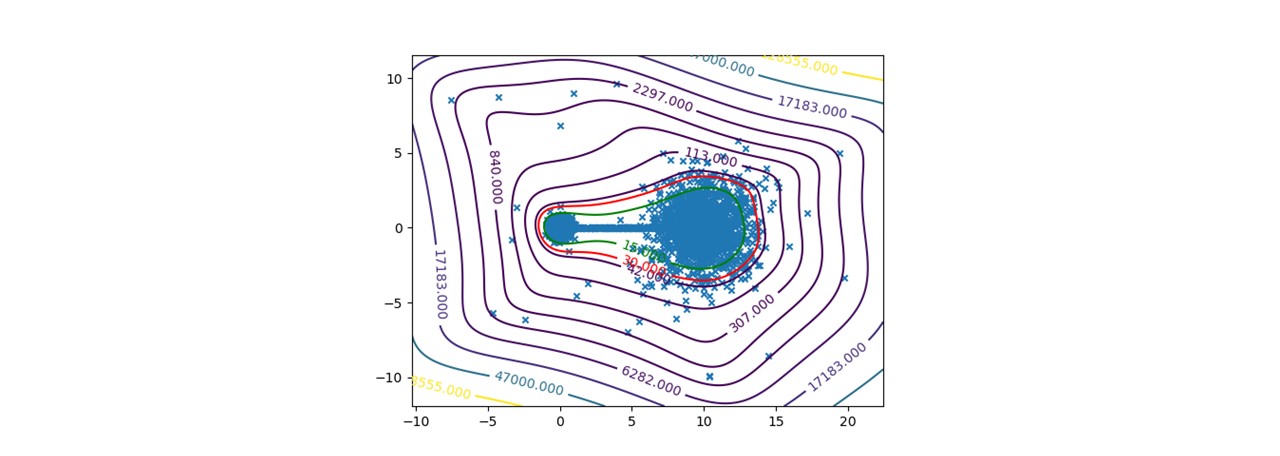
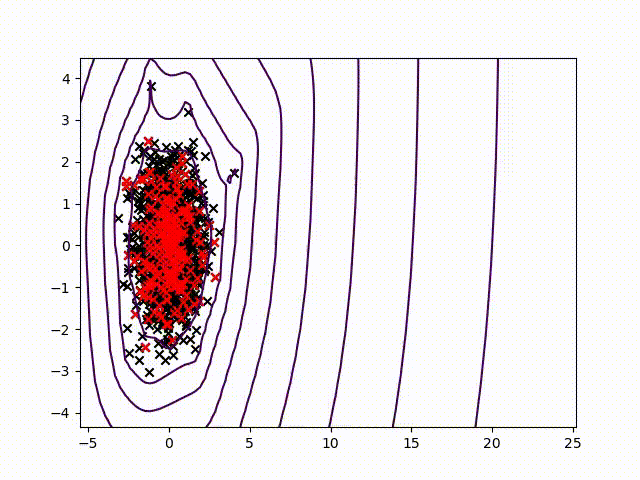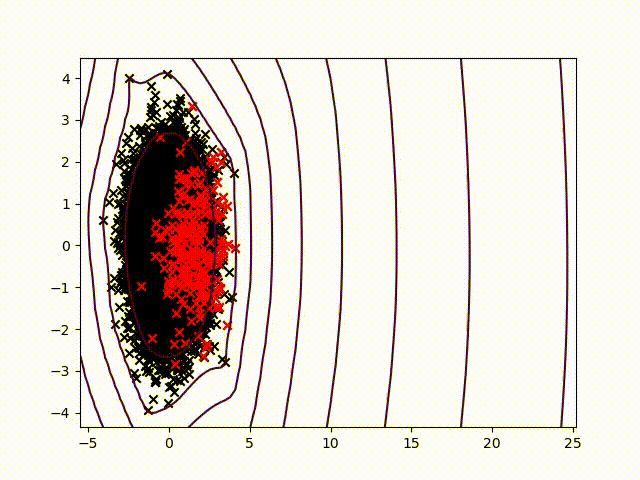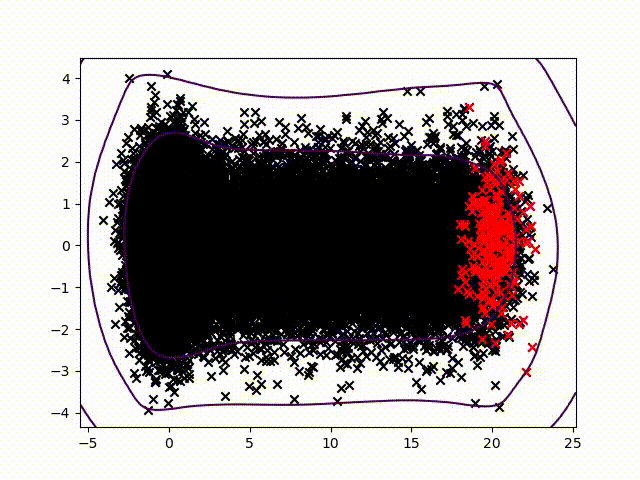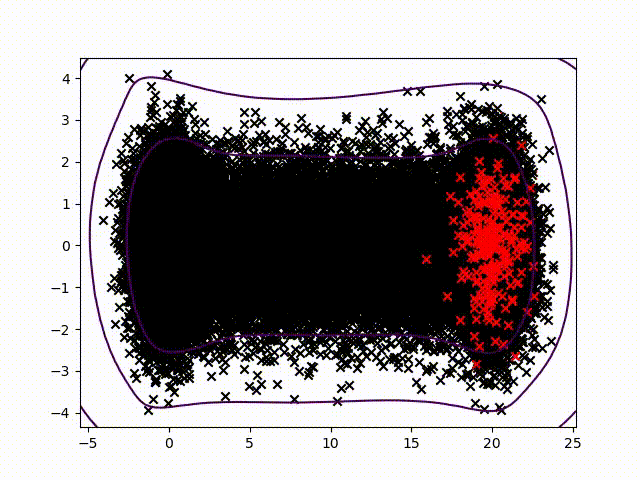
Pour certifier les données des capteurs, nous avons choisi de travailler sur la détection des anomalies qui permettent d'attribuer un taux de normalité pour chaque mesure. Nous avons commencé à travailler sur la méthode présentée dans cet article pour développer une méthode commune, simple à lire et praticable sur tout système industriel sans paramétrage spécifique. Une condition difficile dans l'état de l'art. Nous travaillons sur une méthode utilisant le noyau de Christoffel-Darboux pour obtenir un enveloppement d'un nuage de points. Cette méthode n'a pas été beaucoup utilisée en analyse de données jusqu'à présent, alors qu'elle a de grands atouts dans le domaine de l'analyse de données. séries chronologiques multivariées (pour mesurer un phénomène, une série chronologique multivariée comporte plus d'une variable dépendant du temps. Chaque variable ne dépend pas exclusivement de ses valeurs passées mais a également une certaine dépendance vis-à-vis d'autres variables. Cette dépendance est utilisée pour prévoir les valeurs futures.) détection des anomalies.
Les caractéristiques de cette solution sont:
- Le modèle peut être généré avec un paramètre entier, une qualité/un avantage considérable par rapport aux autres méthodes.
- Le modèle est réactifil peut être mis à jour très rapidement. Avec un faible nombre de variables, le modèle calcule un taux d'observation avant l'arrivée d'une nouvelle variable.
- Alors que la plupart des méthodes ont besoin d'un taux de contamination pour fixer le seuil de décision sur le score, cette méthode met en place un seuil de référence qui dépend du paramètre d et du nombre de variables. Cependant, la qualité du résultat avec ce seuil dépend de l'application et du paramètre d choisi.
- La complexité du calcul ne dépend pas des numéros des observations, mais du nombre de variables et du paramètre d. C'est un grand atout pour le calcul de grandes données avec de petites variables.
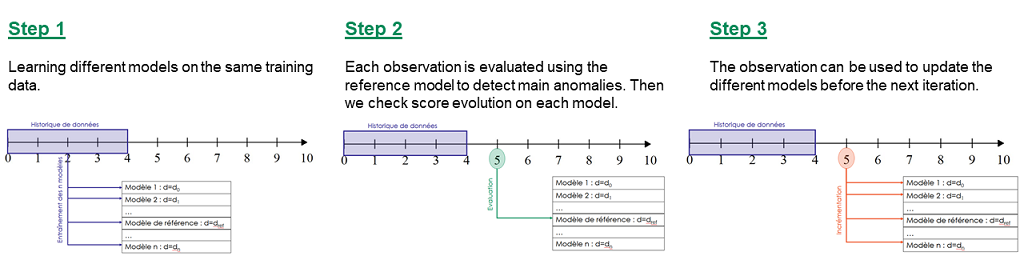
Pour passer la limite du seuil, nous utilisons une autre propriété de la fonction de taux. Si nous générons divers modèles avec différents paramètres d, la croissance du score en fonction de d sera polynomiale pour les points réguliers et exponentielle pour les anomalies. Sur cette base, nous pouvons générer différents modèles et étudier la croissance du score pour prendre une décision sans fixer de seuil.. Même avec la nécessité de mettre à jour les modèles et de mesurer chaque observation, nous maintenons une bonne vitesse de calcul dans cette application.
Quelle est la prochaine étape ?
Des instabilités calculatoires peuvent apparaître en fonction de la standardisation des données, nous travaillons sur ce dysfonctionnement. Nous réaliserons ensuite une publication scientifique sur ce travail et son application sur des données réelles pour avoir des retours sur la méthode.
A suivre...