BL.Optim is a research project of Berger-Levrault about planning management through optimization algorithm. However, the “constraints description” part in BL.Optim is supported by an API, which is extremely difficult to use to express new constraints. We want to replace the constraint descriptor by using a language more or less expressive, which allow us to easily adapt our implementation to others rule-driven problems in the various areas. The relevant problem is the Constraint Satisfaction Programming (CSP)-based optimization problem.
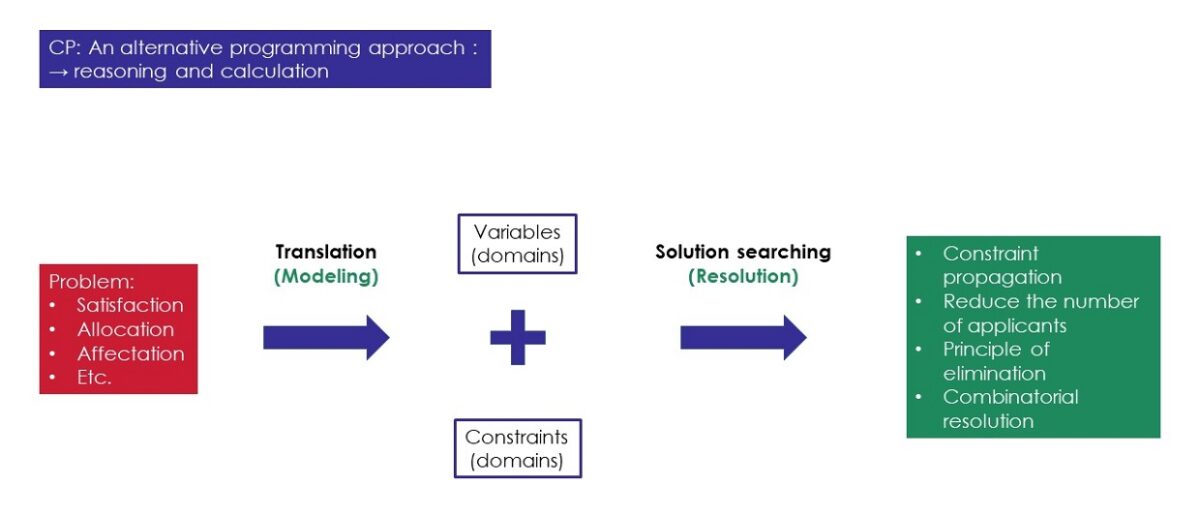
We worked on the formulation and resolution of optimization problems using a domain-specific language (DSL). Before talking about the existing modeling languages and their characteristics, we will talk about CSP, which is an alternative approach of the mathematical programming, combining reasoning and calculations. CSP-based optimization problem is composed of two parts: modeling and resolution.
How to translate the real-life optimization problem into applied mathematic field in order to obtain a decision-making support solution ? At the beginning, we have a problem described by the customer in a native language. Then we translate it through the (modeling) process to obtain a mathematical problem including decision variables and constraints on a precise domain. Finally, in the (resolution) part, the model is written though the use of DSL. We obtain the solution of our problem by submitting the formulated model to a CSP oriented solver.
Figure 1 is a representative schema of solution generation process for an optimization problem:
The conducted study
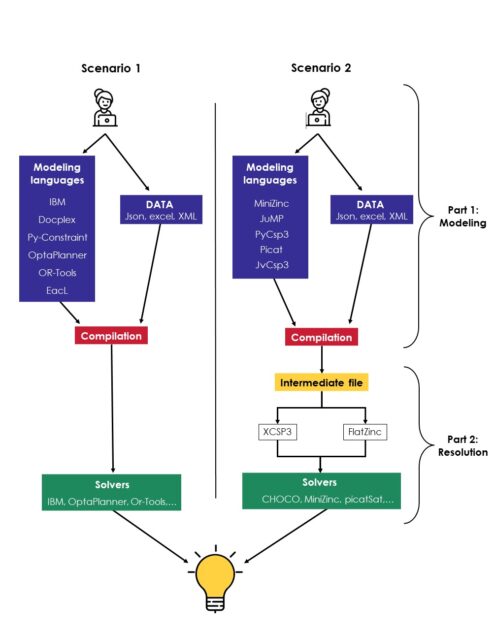
We pushed the research on the two parts of the CSP-based optimization problem, and especially the modeling part. As we said before, we need a DSL for realize the mathematic modeling, and we find more than 20 existing DSLs in full development with rich documentation. We are interested in the 11 DSLs most cited in the literature which are: “IBM-ILOG-OPL”, “Doceplex”, “Py-Constraint”, “OptaPlanner”, “OR-Tools”, “EacL”, “MiniZinc”, “JuMP”, “PyCsp3”, “Picat” and “JvCSP3”. We separated them in two categories :
- the first category refers to the DSL which is embedded in a solver, as shown in Figure 2’s scenario 1, the call to the solver is done directly after the compilation of the data instances and model.
- For the second category, as shown in Figure 2’s scenario 2, an intermediate file is obtained as a result of the compilation of the CSP model. This file contains the models without the solution, and the call to the solver is done afterwards, separately with the modeling part through the use of DSL. For example, for “MiniZinc”, we have a “FlatZinc” as an intermediate file. For “PyCSP3”, a “XCSP3” file is the result of the compilation of model written in “XCSP3”.
As part of this research project, we are more interested in the second scenario because it is the one that will allow us to make the change in the model without having to change the whole functioning of the resolution. Moreover, it will allow us to solve the model by using different solver.
For a better understanding of the two scenarios, we schematized them as follow:
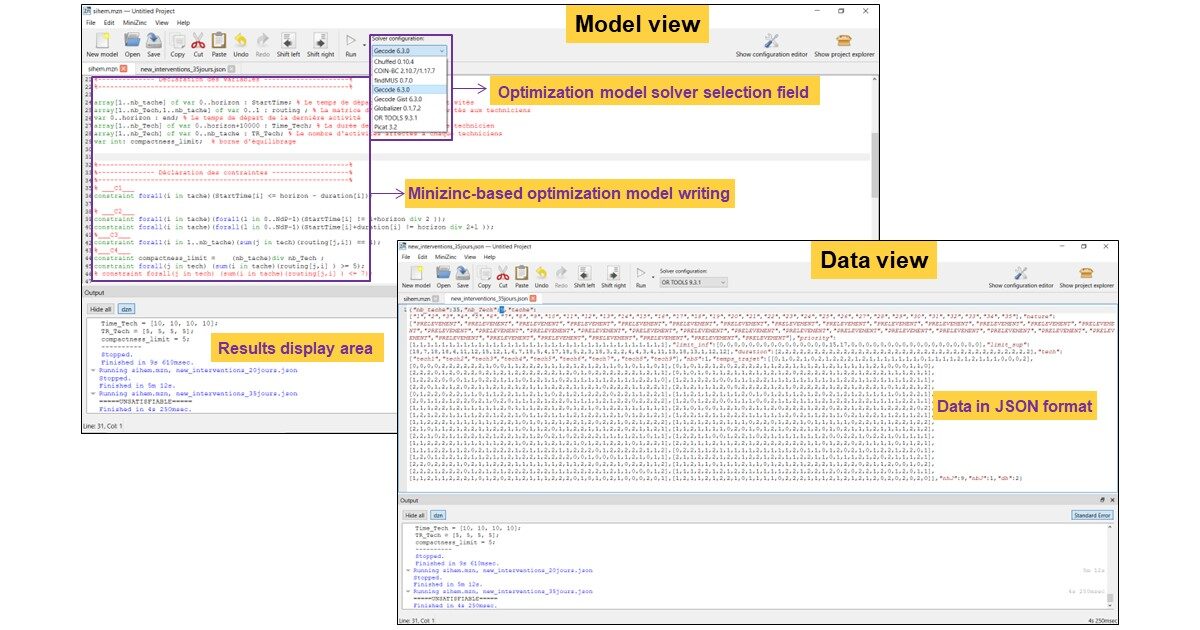
The Preventive Maintenance Scheduling and Routing Problem (PMSRP) is chosen as a use case for the purpose of experimentation. We started the modeling of PMSRP [1] with “MiniZinc” because it is widely used in the literature for solving the problem formulated based on CSP. After compiling the model written in DSL “MiniZinc”, we obtain a flattened file “FlatZinc”. Moreover, we can write complex constraints because when compiling the model, the compiler of “MiniZinc” flattens the constraints in the intermediate output file. The disadvantage that we have encountered so far with this DSL, is that the solvers proposed by the IDE of “MiniZinc” are based on the exact method. To solve our problem with NP-complete complexity, the experiment show that we can solve a problem up to 50 maintenance activities per day, the embedded solvers in IDE of “MiniZinc” (Cf. Figure 3 – IDE “MiniZinc”) can not give us a solution in a reasonable computation time (≥3 hours).
Future works
In the near future, we will do a complete experiment with “MiniZinc”, by using real dataset to be able to test them with different solvers. Then, we will compare the quality of the solutions generated by different solvers with their computing performances. Finally, we will investigate the possibility about the integration of “MiniZinc” DSL into BL.Optim, which will help us to improve the inefficiency regarding the formulation of new business rules under various context.
By Sihem Laradi