We are often brought to solve problems with constraints in real life, such as: shopping in several distant stores, planning and organizing vacation expenses, or packing things in boxes during a move. Resolving these problems with constraints is not always easy. More particularly, when it comes to optimizing a set of criteria such as time, cost, or space. For many problems, the set of possible solutions is very large, making it impossible to compare possible solutions in a reasonable time. Automation of the resolution is therefore necessary even if it represents also a real challenge for machines.
What are Constraint Satisfaction Problems?
This type of problem is widely investigated in the literature under the name of « Constraint Satisfaction Problem (CSP)» [1,3–6], which is formally defined by a triplet (X, D, C) where :
- X = {X_1,X_2,…,X_N} is a set of variables of the problem.
- D is a domain function that associates to each Xi its domain D(X_i) (possible values of X_i).
- C = {C_1,C_2,…,C_M} is a set of constraints of the problem.
A constraint is defined by a couple (V,R) where:
- V = {V_1,V_2,…,V_R} is the set of variables related to the constraint.
- R is a relation which defines the set of tuples satisfying the constraint.
To define a problem as a CSP, we need to answer three key questions:
- What is the set of variables of our problem?
- What is the domain of each variable of our problem?
- And how to define a constraint?
We have already answered these three questions for a home care services planning optimization problem [2] and a problem of planning optimization of material and human resources for maintenance interventions. We detail in this article the language that we proposed to define the constraints.
A Constraint Language for CPS
We proposed a flexible and expressive language to represent the constraints in the form of predicates that can include variables, constants, and functions of the problem.
A constraint concerns a variable V, it is defined by a set of restriction rules applied to the variable V. The combination of these restriction rules produces a very expressive language for constructing constraints. This language must be carefully defined, the more the language is expressive, the more it allows to represent more constraints, but the evaluation of these constraints will difficult and longer. The less the language is expressive, the less the possibility of expressing constraints, but the evaluation of these constraints will easy and rapid.
Definition of a constraint
A constraint is defined by a couple:
- V is the variable concerned by the constraint, each constraint concerns one variable.
- R=(R_1,R_2,…,R_N) is the set of restriction rules applied to the variable V.
A restriction rule R is defined to restrict the domain of a variable V. This restriction is carried out by four possible operators : “greater than” to select values greater than the operand, “less than” to select values less than the operand, “equal to” to redefine the domain of the variable with a set of operands and “different from” to select values different to the set of operands. The operands of an operator can be constants, variables of the CSP or the combination of both.
A restriction rule is only applied if all conditions associated with the rule are “true”.
A restriction rule R is defined by a quadruplet (T,RC,RV,D):
- T is the type of the restriction rule.
- RC=( RC1, RC2,…, RCM) is the set of constants of the restriction rule.
- RD=(RD1, RD2,…, RDP) is the set of variables of the restriction rule.
- D=(D1,D2,…, DZ) is the set of conditions of the restriction rule.
The conditions of a restriction rule are used when the application of the restriction rule depends on the value of another variable of the problem. The conditions are evaluated when assigning the variable to redefine its domain.
A condition is defined by a triplet :
- T is the type of condition.
- OC=(OC1, OC2,…, OCM) is the set of constants of the condition.
- OV=(OV1, OV2,…, OVM) is the set of variables of the condition.
Implementation of a constraint
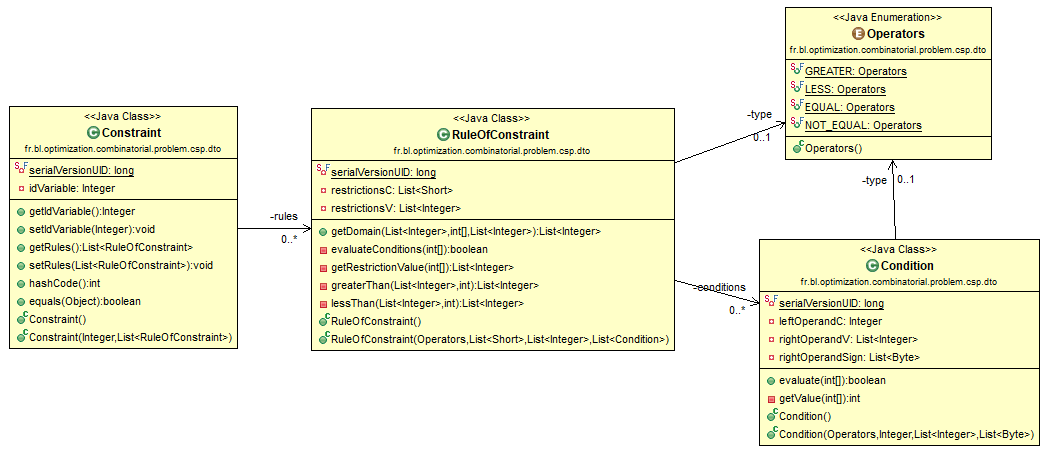
Constraints are implemented as Java classes (Figure 1):
- Constraint class: it is the main class. It contains the variable concerned by the constraint and the set of restriction rules associated with the variable.
- RuleOfConstraint class: it allows us to define the rules allowing us to restrict the domain of the variable. It is defined by its operator, its operands and a set of conditions to be checked before the evaluation of the rule. It also contains the “getDomain (…)” function which evaluates the rule to return the new domain of the variable.
- Condition class: it defines the condition to be satisfied before the evaluation of a restriction rule. It is defined by a condition operator and a set of operands (constant and variables).
All the constraints of the context of home care services planning or maintenance interventions planning can be expressed with our implementation.

Conclusion & Perspective
In summary, we proposed a constraint language to define the constraints of a CSP. This language covers a family of sub-languages of first-order logic. It allows us to deal with all the constraints encountered in the context of home care services planning or maintenance interventions planning.
The next objective of our work is to prove that our constraint language allows to express all the constraints of a CSP. We plan to define metrics on the constraints to improve the variable selection strategy and to work on the mechanism of evaluation of the constraints to improve it. We will also look at what is done on CSPs in terms of filtering variables domains, representation and constraints management.
References
[1] Sally C Brailsford, Chris N Potts, and Barbara M Smith. 1999. Constraint satisfaction problems: Algorithms and applications. Eur. J. Oper. Res. 119, 3 (1999), 557–581.
[2] Yahia Chabane, Christophe Bortolaso, and Mustapha Derras. 2019. When ants take care of humans: ACO for home-care services planning optimization. In Studies in Health Technology and Informatics.
[3] Christodoulos A Floudas and Panos M Pardalos. 1990. A Collection of Test Problems for Constrained Global Optimization Problems. Springer.
[4] Kim. Marriott and P J Stuckey. 1998. Programming with constraints : an introduction. MIT Press Cambridge, Mass.
[5] Francesca Rossi, Peter van Beek, and Toby Walsh (Eds.). 2006. Handbook of Constraint Programming. Elsevier.
[6] Christine Solnon. 2010. Ant Colony Optimization and Constraint Programming. Wiley.